
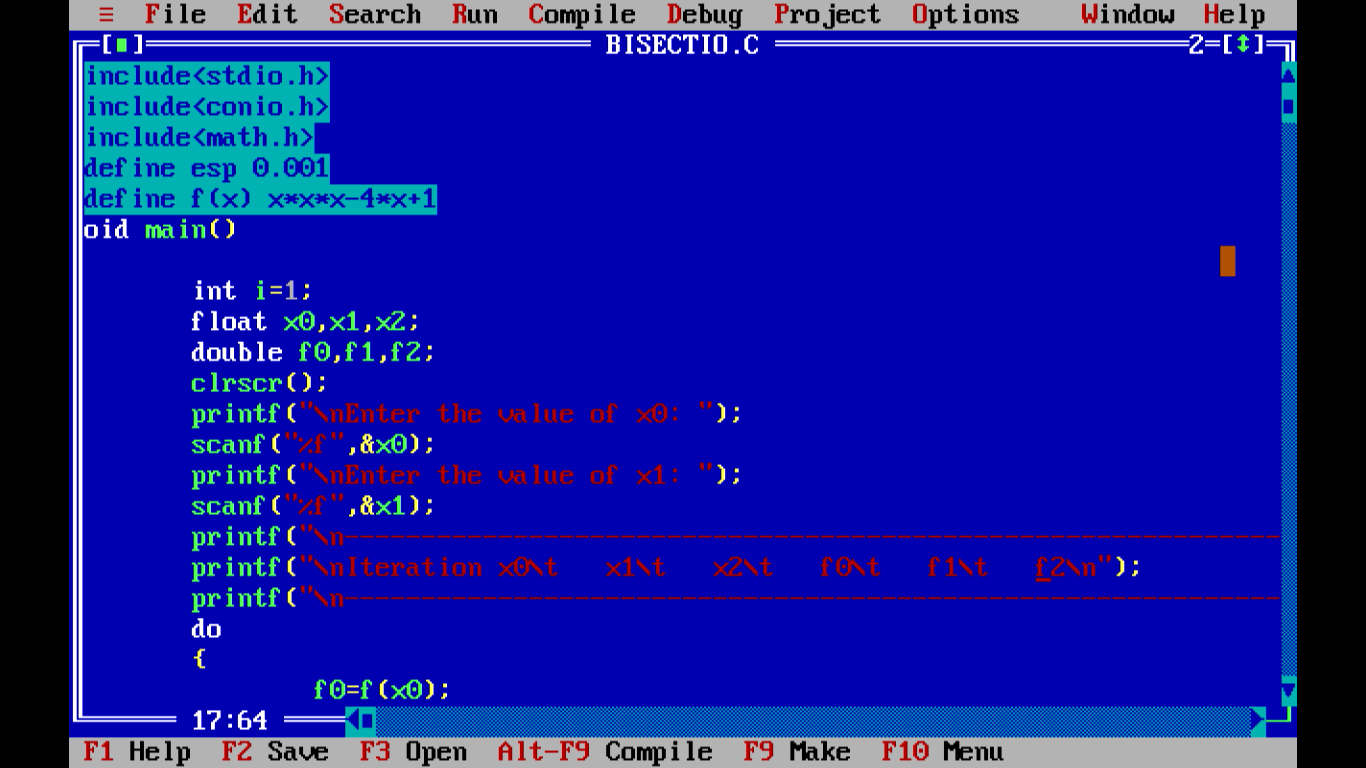
When implementing the method on a computer, there can be problems with finite precision, so there are often additional convergence tests or limits to the number of iterations. Examine the sign of f(c) and replace either (a, f(a)) or (b, f(b)) with (c, f(c)) so that there is a zero crossing within the new interval. If convergence is satisfactory (that is, a - c is sufficiently small, or f(c) is sufficiently small), return c and stop iterating.

Calculate the function value at the midpoint, f(c). Each iteration performs these steps: Calculate c, the midpoint of the interval, c = a + b/2. The function values are of opposite sign (there is at least one zero crossing within the interval). The process is continued until the interval is sufficiently small.Įxplicitly, if f(a) and f(c) have opposite signs, then the method sets c as the new value for b, and if f(b) and f(c) have opposite signs then the method sets c as the new a. Fisher Price Time To Play Dollhouse Downloads. In this way an interval that contains a zero of f is reduced in width by 5. Unless c is itself a root (which is very unlikely, but possible) there are now only two possibilities: either f(a) and f(c) have opposite signs and bracket a root, or f(c) and f(b) have opposite signs and bracket a root. At each step the method divides the interval in two by computing the midpoint c = (a+b) / 2 of the interval and the value of the function f(c) at that point. Libro Contabilidad Financiera Pdf Download on this page. Descargar Roxio Creator Plus Dell Edition Definition there. In this case a and b are said to bracket a root since, by the intermediate value theorem, the continuous function f must have at least one root in the interval (a, b). Return to Numerical Methods - Numerical Analysis. Computer Programming Fortran program code for newton raphson. 9.1 Bracketing and Bisection 343 9.2 Secant Method. 1.1 Program Organization and Control Structures 5.
9.2 Secant Method, False Position Method, and Ridders’ Method 347 Sample page from NUMERICAL RECIPES IN FORTRAN 77. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods.įORTRAN77 Source Codes. It is a very simple and robust method, but it is also relatively slow. The bisection method in mathematics is a root- finding method that repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. The bigger red dot is the root of the function. For searching a finite sorted array, see binary search algorithm. This article is about searching continuous function values. Program For Bisection Method In Fortran 77 5,0/5 5852 reviewsīisection method - Wikipedia.


 0 kommentar(er)
0 kommentar(er)
